Fracciones – Presentación, ejercicios e imagenes para el aula
Hola Compañer@s, como están? Les dejo mucha info sobre fracciones para sus clases.
Espero les sirva el material!
Fracciones
Una fracción es una parte de un total
Corta una pizza en trozos, y tendrás fracciones:
 |
 |
 |
1/2 |
1/4 | 3/8 |
|
(Una mitad)
|
(Un cuarto)
|
(Tres octavos)
|
| El número de arriba te dice cuántas porciones tienes y el de abajo te dice en cuántos trozos se ha cortado la pizza. | ||
Numerador / Denominador
Al número de arriba lo llamamos Numerador, es el número de partes que tienes.
Al de abajo lo llamamos Denominador, es el número de partes en que se ha dividido el total.
| Numerador |
| Denominador |
¡Sólo tienes que recordar esos nombres! (Si los confundes, recuerda que denominador es con “D” de dividir)
Fracciones equivalentes
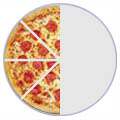
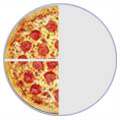
Algnas fracciones parecen diferentes pero en realidad son la misma, por ejemplo:
| 4/8 | = | 2/4 | = | 1/2 | ||
| (Cuatro octavos) | (Dos cuartos) | (Una mitad) | ||||
 |
 |
 |
Normalmente lo mejor es dar la respuesta usando la fracción más simple (1/2 en este caso). Eso se llamaSimplificar o Reducir la fracción.
Sumar fracciones
Puedes sumar fracciones fácilmente si el número de abajo (el denominador) es el mismo:
| 1/4 | + | 1/4 | = | 2/4 | = | 1/2 | ||
| (Un cuarto) | (Un cuarto) | (Dos cuartos) | (Una mitad) | |||||
 |
 |
 |
 |
Otro ejemplo:
| 5/8 | + | 1/8 | = | 6/8 | = | 3/4 | ||
 |
 |
 |
 |
Sumar fracciones con denominadores diferentes
¿Y si los denominadores no son iguales? Como en este ejemplo:
| 3/8 | + | 1/4 | = | ? | ||||
 |
 |
 |
 |
Deberías hacer que los denominadores fueran iguales de alguna manera. En este caso es fácil, porque sabemos que 1/4 es lo mismo que 2/8 :
| 3/8 | + | 2/8 | = | 5/8 | ||||
 |
 |
 |
 |
Fracciones Equivalentes
Las Fracciones Equivalentes tienen el mismo valor, aunque parezcan diferentes.
Estas fracciones son en realidad lo mismo:
| 1 | = | 2 | = | 4 |
| – | – | – | ||
| 2 | 4 | 8 |
¿Por qué son lo mismo? Porque cuando multiplicas o divide a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
¡Lo que haces a la parte de arriba de la fracción
también lo tienes que hacer a la parte de abajo!
Por eso, estas fracciones son en realidad la misma:
| × 2 | × 2 | |||
|
|
||||
| 1 | = | 2 | = | 4 |
| – | – | – | ||
| 2 | 4 | 8 | ||
|
|
||||
| × 2 | × 2 | |||
Y en un dibujo se ve así:
| 1/2 | 2/4 | 4/8 | ||
 |
= |  |
= |  |
Aquí hay más fracciones equivalentes, esta vez dividiendo:
| ÷ 3 | ÷ 6 | |||
| 18 | = | 6 | = | 1 |
| 36 | 12 | 2 | ||
| ÷ 3 | ÷ 6 | |||
Si seguimos dividiendo hasta que no podamos más, habremos simplificado la fracción (la hemos hecho la más simple posible).
Importante:
- Las partes de arriba y abajo de la fracción siempre deben ser números enteros.
- Las operaciones que podemos hacer son multiplicar y dividir (siempre las dos partes a la vez). Si sumamos o restamos un número arriba y abajo, no tendremos una fracción equivalente.
- El número que elijas para dividir las dos partes no debe dejar ningún resto en las divisiones.

Aprende Las Fracciones
Una fracción, en general, es la expresión de una cantidad dividida por otra, y una fracción propia representa las partes que tomamos de un todo.
El ejemplo clásico es el de un queso que partimos en porciones. En el dibujo, hemos hecho 8 porciones, 3 rosas y 5 verdes.
| Si tomamos las 3 rosas, representan 3 porciones de las ocho en las que hemos dividido el queso, es decir 3 / 8 del queso, y si tomamos las 5 verdes, representan 5 porciones de las ocho en las que hemos dividido el queso, es decir 5 / 8 del queso. |
 |
Las partes que tomamos ( 3 ó 5 ) se llaman numerador y las partes en que dividimos el queso ( 8 ) denominador.
Para leer una fracción, el numerador se lee normalmente pero, como veremos a continuación, el denominador tiene una forma especial de leerse.
| Denominador | Lectura | Ejemplos |
| 2 | medios | 5 / 2 = cinco medios |
| 3 | tercios | 2 / 3 = dos tercios |
| 4 | cuartos | 3 / 4 = tres cuartos |
| 5 | quintos | 4 / 5 = cuatro quintos |
| 6 | sextos | 5 / 6 = cinco sextos |
| 7 | séptimos | 6 / 7 = seis séptimos |
| 8 | octavos | 7 / 8 = siete octavos |
| 9 | novenos | 8 / 9 = ocho novenos |
| 10 | décimos | 9 / 10 = nueve décimos |
| mayor de 10 | Se agrega al número la terminación avos |
10 / 11 = diez onceavos
|
Clasificación De Las Fracciones
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.
| Tipo | Características | Ejemplos |
| Propia | El numerador es menor que el denominador | 1 / 2, 7 / 9 |
| Impropia | El numerador es mayor que el denominador | 4 / 3, 5 / 2 |
| Homogéneas | Tienen el mismo denominador | 2 / 5, 4 / 5 |
| Heterogéneas | Tienen distinto denominador | 3 / 7, 2 / 8 |
| Entera |
El numerador es igual al denominador;
representan un entero
|
6 / 6 = 1 |
| Equivalentes |
Cuando tienen el mismo valor.
Dos fracciones son equivalentes
si son iguales sus productos cruzados
|
2 / 3 y 4 / 6
2 x 6 = 3 x 4 |
Si en una fracción multiplicamos o dividimos el numerador y el denominador por un mismo numero, obtenemos una fracción equivalente a la primera, pues ambas tienen el mismo valor. Por ejemplo:
| 1 | (1 x 4) | 4 | 3 | (3 : 3) | 1 | |||||||||
| — | = | ——— | = | — | = | 0,5 ; | — | = | ——— | = | — | = | 0,2 | |
| 2 | (2 x 4) | 8 | 15 | (15 : 3) | 5 |
Simplificar o Reducir una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, lo primero que hacemos es buscar el mayor número que divide exactamente (resto = 0) al numerador y al denominador (mayor divisor común) y después dividimos el numerador y el denominador por este mayor divisor común, ya que como hemos visto antes, dividiendo el numerador y el denominador de una fracción por un mismo número obtenemos una fracción equivalente (de igual valor).
Por ejemplo: Simplificar 30/42
Los números que dividen exactamente a 30 (divisores) son: 2, 3, 5, 6, 10 y 15.
Los números que dividen exactamente a 42 (divisores) son: 2, 3, 6, 7, 14 y 21.
Los divisores comunes a ambos son 2, 3 y 6. El mayor divisor común es 6, por tanto, dividimos numerador y denominador por 6.
| 30 | 30/6 | 5 | ||
| —— | = | ——— | = | — |
| 42 | 42/6 | 7 |
Cuando en una fracción, el numerador y el denominador no tienen ningún divisor común, se dice que es una fracción irreducible.
Suma Y Resta De Fracciones
Si las fracciones tienen el mismo denominador (homogéneas), se suman o restan los numeradores y se pone el mismo denominador.
Ejemplo:
| 3 | 2 | (3 + 2) | 5 | 5 | 2 | (5 – 2) | 3 | |||||||
| — | + | — | = | ——— | = | — | ; | — | – | — | = | ——— | = | — |
| 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 |
Si las fracciones tienen distinto denominador (heterogéneas), lo primero que tenemos que hacer es igualar los denominadores. Para conseguirlo, buscamos dos fracciones equivalentes a las dadas, multiplicando el numerador y el denominador de cada una de ellas por el denominador de la otra. Una vez obtenido el mismo denominador, procedemos como en el caso anterior, sumamos los numeradores y ponemos el denominador común.
Ejemplo:
| 2 | 3 | (2 x 7) | (3 x 5) | 14 | 15 | 29 | ||||||
| — | + | — | = | ——— | + | ——— | = | —— | + | —— | = | —— |
| 5 | 7 | (5 x 7) | (7 x 5) | 35 | 35 | 35 |
Multiplicación De Fracciones
El producto de varias fracciones es igual a otra fracción que tiene por numerador el producto de los numeradores y por denominador el producto de los denominadores.
Ejemplo:
| 3 | 4 | 2 | (3 x 4 x 2) | 24 | 2 | ||||||
| — | x | — | x | — | = | ———— | = | —— | simplificando | = | — |
| 4 | 5 | 3 | (4 x 5 x 3) | 60 | 5 |
Fracción De Un Número
Calcular la fracción de un número es lo mismo que multiplicar la fracción por ese número.
Ejemplo: Calcular los 2 / 3 de 60:
| 2 | 2 | (2 x 60) | 120 | |||||||||
| — | de | 60 | = | — | x | 60 | = | ——— | = | —— | = | 40 |
| 3 | 3 | 3 | 3 |
División De Fracciones
El cociente de dos fracciones es otra fracción que tiene por numerador el producto del numerador de la primera por el denominador de la segunda, y por denominador el producto del denominador de la primera por el numerador de la segunda.
Ejemplo:
| 4 | 3 | (4 x 5) | 20 | |||
| — | : | — | = | ——— | = | —— |
| 9 | 5 | (9 x 3) | 27 |
.
Ejercicios:
A. Simplifique las siguientes Fracciones.
| 1. 3 6 |
2. 15 45 |
3. 4 9 |
| 4. 2 8 |
5. 6 12 |
6. 12 48 |
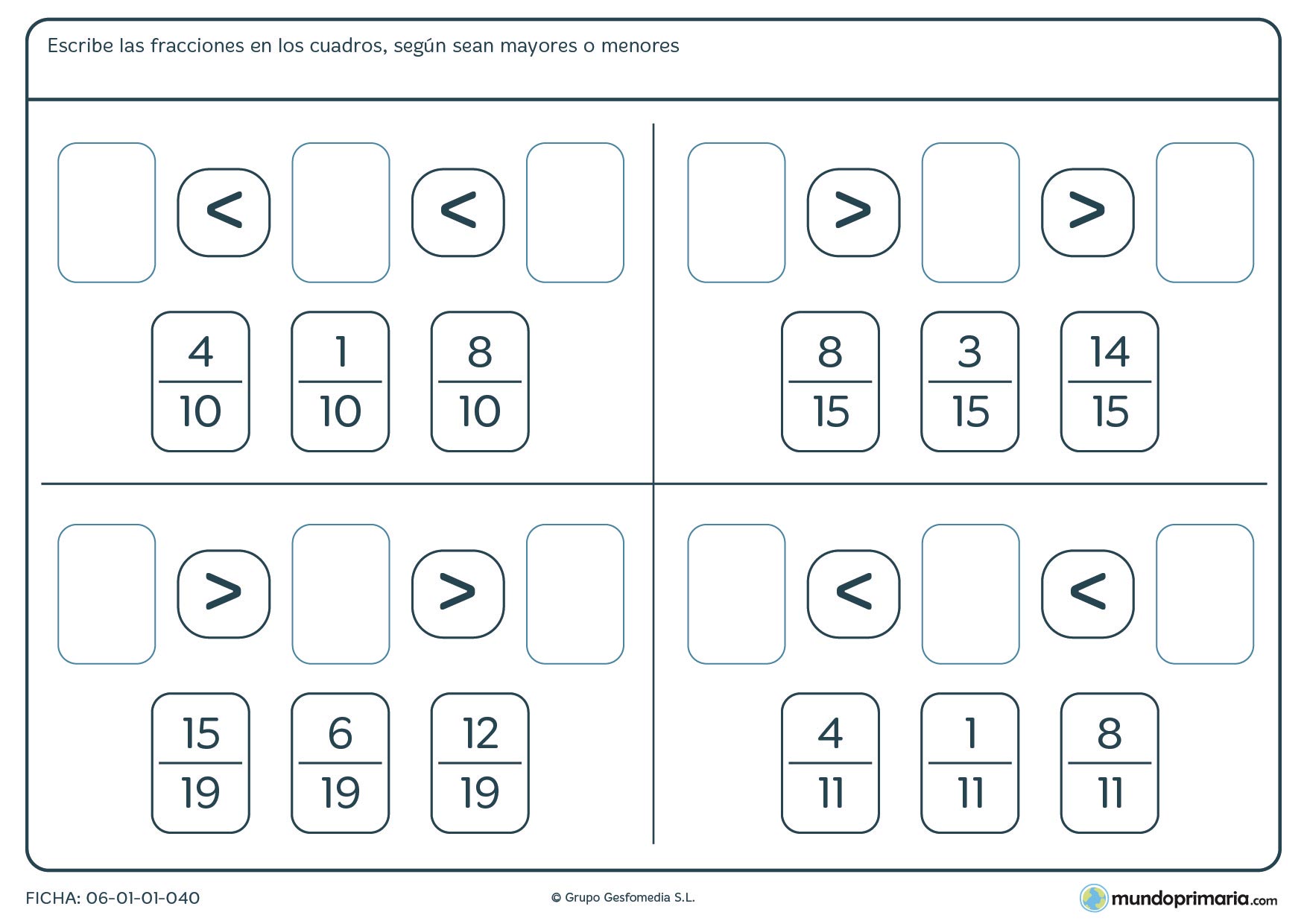
B. Indique cuál fracción es mayor. ( Utiliza el signo de >, <)
| 7. 62 11 9 |
8. 46 11 7 |
| 9. 412 9 17 |
10. 49 3 2 |
C. Suma las siguientes fracciones.
| 11. 9 + 1 5 5 |
12. 2 + 5 3 3 |
| 13. 1 + 2 2 3 |
14. 5 + 1 6 5 |
| 15. 3 + 1 7 2 |
16. 1 1 + 2 1 8 4 |
| 17. 9 + 5 11 7 |
18. 3 + 4 2 3 |
D. Resta las siguientes fracciones.
| 19. 6 – 1 7 7 |
20. 6 – 1 11 2 |
| 21. 4 – 5 3 2 |
22. 5 – 1 8 8 |
| 23. 9 – 1 11 5 |
24. 2 1 – 1 1 5 4 |
| 25. 3 – 1 4 2 |
26. 7 – 1 9 3 |
Soluciones:
1. 1/2; 2. 1/3; 3. 4/9; 4. 1/4; 5. 1/2; 6. 1/4 ; 7. > ; 8. >; 9. < ; 10. < ; 11. 2 ; 12. 1 1/6 13. 1 1/6 ; 14. 1 1/30
15. 3 ; 16. 3 3/8 17. 118/77 18. 1/6 19. 5/7 20. 1/22 21. -7/6 22. 1/2 23. 34/55 24. 19/20 ; 25. 1/4 ; 26. 4/9.
Ejercicios: Simplifica, suma y resta de fracciones
1: 3/21
2: 14/20
3: 12/24
4: 6/10
5: 6/14
6: 6/22
7: 6/8
8: 6/21
9: 21/24
10: 2/18
11: 4/16
12: 14/18
1: 3/7 + 2/7
2: 1/7 + 3/7
3: 4/8 + 3/8
4: 5/7 + 1/7
5: 1/3 + 1/3
6: 1/9 + 4/9
7: 5/8 + 2/8
8: 2/4 + 1/4
9: 5/9 + 3/9
10: 4/7 + 2/7
11: 1/6 + 1/6
12: 3/9 + 4/9
13: 3/6 + 2/6
14: 3/8 + 3/8
15: 2/8 + 3/8
1: 1/6 + 1/11
2: 1/10 + 1/8
3: 1/10 + 1/12
4: 1/8 + 1/11
5: 1/5 + 1/9
6: 1/2 + 1/6
7: 1/11 + 1/10
8: 1/7 + 1/10
9: 1/11 + 1/2
10: 1/6 + 1/4
11: 1/2 + 1/12
12: 1/11 + 1/4
13: 1/5 + 1/7
14: 1/8 + 1/12
15: 1/9 + 1/4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
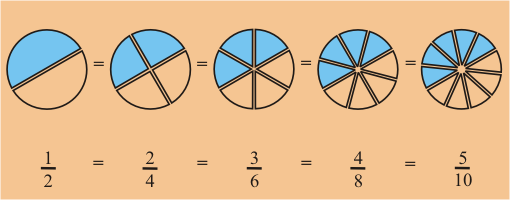
Fuente:
http://www.disfrutalasmatematicas.com/numeros/fracciones.html
http://www.elabueloeduca.com/aprender/matematicas/fracciones/fracciones.html
Espero les sea de utilidad y que también puedan compartir sus actividades con la comunidad y redes sociales!
No olvides puntuar la publicación y dejar un comentario!