Polinomios para Primaria y Secundaria Inicial
📚 Polinomios para Primaria y Secundaria Inicial
📖 Teoría
Un polinomio es una expresión matemática formada por la suma o resta de términos que incluyen números y letras (llamadas variables o incógnitas), elevadas a exponentes enteros no negativos.
Ejemplo: 3x² + 2x + 5
– 3x² → término cuadrático.
– 2x → término lineal.
– 5 → término independiente.
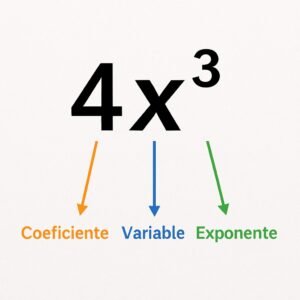
Cada término de un polinomio se compone de:
– Coeficiente: el número que acompaña a la variable.
– Variable: la letra que representa un número.
– Exponente: el número que indica cuántas veces se multiplica la variable por sí misma.
Clasificación de polinomios según sus términos:
1. Monomio: un solo término (ejemplo: 7x).
2. Binomio: dos términos (ejemplo: x + 5).
3. Trinomio: tres términos (ejemplo: x² + 2x + 1).
4. Polinomio de más de tres términos (ejemplo: 2x³ + x² + 5x + 7).
El grado de un polinomio es el exponente más alto de la variable.
Ejemplo: En 4x³ + 2x² + 7, el grado es 3.
Operaciones básicas:
– Suma y resta: se suman o restan términos semejantes.
Ejemplo: (2x² + 3x) + (x² + 5x) = 3x² + 8x.
– Multiplicación: cada término se multiplica con los del otro polinomio.
Ejemplo: (x + 2)(x + 3) = x² + 5x + 6.
Los polinomios son fundamentales en matemáticas y su comprensión abre el camino hacia temas más avanzados como la factorización, las ecuaciones y el estudio de funciones. También aparecen en áreas como geometría, física y economía.
🖼️ Imágenes representativas
- Un gráfico que muestre la estructura de un polinomio con coeficiente, variable y exponente.
- Ejemplos de monomio, binomio y trinomio.

- Una curva sencilla representando un polinomio en el plano cartesiano.
✏️ Práctica: 5 Casos con 3 ejemplos cada uno y sus respuestas
🧮 Caso 1: Identificar las partes de un polinomio
Ejemplos:
-
5x² + 2x + 1
-
3x + 7
-
4x³ – 2x + 5
Respuestas:
-
Coeficientes: 5, 2, 1 → Variables: x², x → Término independiente: 1
-
Coeficientes: 3, 7 → Variable: x → Término independiente: 7
-
Coeficientes: 4, -2, 5 → Variables: x³, x → Término independiente: 5
➕ Caso 2: Clasificar polinomios según su cantidad de términos
Ejemplos:
-
6x →
-
x² + 3x →
-
2x³ + 4x + 1 →
Respuestas:
-
Monomio
-
Binomio
-
Trinomio
✖️ Caso 3: Evaluar polinomios reemplazando la variable
Ejemplos:
-
P(x) = x + 3, si x = 2
-
P(x) = 2x² + 1, si x = 3
-
P(x) = x² + 2x + 3, si x = 1
Respuestas:
-
P(2) = 2 + 3 = 5
-
P(3) = 2(9) + 1 = 19
-
P(1) = 1 + 2 + 3 = 6
➖ Caso 4: Sumar o restar polinomios
Ejemplos:
-
(3x + 2) + (2x + 5)
-
(4x² + x) – (2x² + 3x)
-
(x³ + 2x) + (x³ + 3x + 1)
Respuestas:
-
5x + 7
-
(4x² – 2x²) + (x – 3x) = 2x² – 2x
-
(x³ + x³) + (2x + 3x) + 1 = 2x³ + 5x + 1
📏 Caso 5: Aplicar polinomios a una situación real
Ejemplos:
-
Un rectángulo tiene lados de longitud x y 3. Escribe el polinomio que representa su perímetro.
-
El área de un cuadrado es x². Si el lado aumenta en 2 unidades, ¿cómo se expresa el nuevo área?
-
Si un niño tiene x canicas y su amigo tiene 2x + 3, ¿cuántas tienen juntos?
Respuestas:
-
P = 2x + 6
-
(x + 2)² = x² + 4x + 4
-
Total = x + (2x + 3) = 3x + 3
📌 Conclusión
Los polinomios son expresiones matemáticas fundamentales que ayudan a describir relaciones y resolver problemas en distintas áreas. Reconocer sus partes, clasificarlos y operar con ellos permite a los alumnos fortalecer sus bases de álgebra.
Te adjunto un documento para imprimir con explicacion y ejercicios Click!!
Espero les sea de utilidad y que también puedan compartir sus actividades con la comunidad y redes sociales!
Tambien agredezco tu participacion al puntuar y dejarme un comentario !







Publicar comentario
Lo siento, debes estar conectado para publicar un comentario.