Triángulos
 | Un triángulo tiene tres lados y tres ángulos
|
 | Los tres ángulos siempre suman 180° |
Equilátero, isósceles y escaleno
Hay tres nombres especiales de triángulos que indican cuántos lados (o ángulos) son iguales.
Puede haber 3, 2 o ningún lados/ángulos iguales:
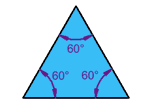 | Triángulo equiláteroTres lados iguales
Tres ángulos iguales, todos 60° |
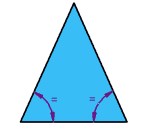 | Triángulo isóscelesDos lados iguales
Dos ángulos iguales |
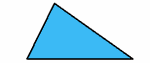 | Triángulo escalenoNo hay lados iguales
No hay ángulos iguales |
¿Qué tipos de ángulos?
Los triángulos también tienen nombres que te dicen los tipos de ángulos
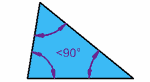 | Triángulo acutánguloTodos los ángulos miden menos de 90° |
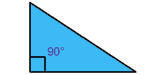 | Triángulo rectánguloTiene un ángulo recto (90°) |
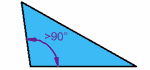 | Triángulo obtusánguloTiene un ángulo mayor que 90° |
Combinar los nombres
A veces los triángulos tienen dos nombres, por ejemplo: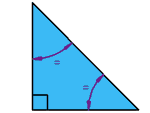 | Triángulo isósceles rectánguloTiene un ángulo recto (90°), y los otros dos ángulos iguales
¿Adivinas cuánto miden? |
Área
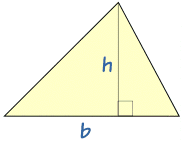 |
Área = ½bh |
La fórmula (1/2)bh vale para todos los triángulos. Asegúrate de que la "h" la mides perpendicularmente a la "b".
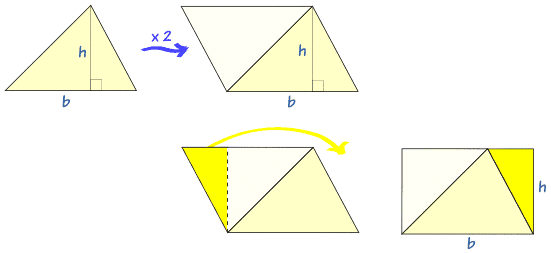
Imagina que "doblas" el triángulo (volteándolo a lo largo de uno de los lados de arriba) para tener una figura de cuatro lados (que será en realidad un "paralelogramo"), entonces el área sería bh. Pero eso son dos triángulos, así que uno solo es (1/2)bh.
Los triángulos tienen 180°
Ha una manera de probar que los ángulos de un triángulo suman 180°:
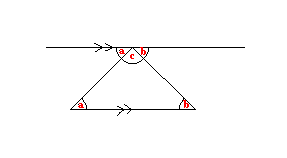
Explicación 1: La línea de arriba (la que toca la punta del triángulo) es paralela a la base. Así que:
- los ángulos "a" son iguales, y
- los ángulos "b" son iguales,
y está claro que "a" + "b" + "c" son un giro desde un lado del triángulo al otro, así que son 180°
Explicación 2: Por las propiedades de los ángulos, cuando una línea corta a dos paralelas se puede ver que los ángulos del triángulo a + b + c = el ángulo sobre una línea recta = 180°
¿
Qué es un Triangulo?, Un triangulo es un polígono que tiene
tres lados, está determinado por
tres lados o tres puntos no alineados llamados
vértices.

El triangulo es una figura plana que no tiene volumen, tiene área, la fórmula para determinar el área es (Basepor altura sobre 2). Laaltura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).
Los lados de un triángulo se escriben en minúscula, con las mismas letras de los vértices opuestos.
Los vértices de un triángulo se escriben con letras mayúsculas.
Los ángulos de un triángulo se escriben igual que los vértices.
Tipos de triángulos.
Los triángulos se pueden clasificar según sus lados en equilátero, isósceles y escaleno, también de acuerdo a sus ángulos internos en acutángulos, rectángulos y obtusángulos.
Propiedades de los triángulos 1 Un lado de un triángulo siempre es menor que la suma de los dos restantes y mayor que su diferencia.
2 La suma de los ángulos interiores del triángulo siempre es igual a 180°.
3 El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
Tipos de triángulos:
1)
Según sus lados Triángulo equilátero: sus tres lados son del mismo tamaño, quiere decir que los tres ángulos internos miden 60 grados.
 Triángulo isósceles
Triángulo isósceles: se reconoce este triángulo si tiene dos lados iguales, o sea de la misma logitud. Además, los ángulos que se oponen a estos lados son de la misma medida.
 Triángulo escaleno
Triángulo escaleno: este triángulo tiene sus tres lados desiguales; no hay dos ángulos que sean de la misma medida.

2)
Según sus ángulos Un triángulo es oblicuángulo cuando sus ángulos interiores no son rectos, es decir,ninguno mide 90º. Esto quiere decir que los triángulosacutángulosy obtusángulosson también oblicuángulos.Veamos:
Triángulos Acutángulos: se reconoce un triángulo acutángulo porque sus tres ángulos son agudos, es decir, son menores de 90º
 Triángulos Rectángulos
Triángulos Rectángulos: Se diferencia en que uno de sus ángulos es recto, o sea, mide 90º
 Triángulos Obtusángulos
Triángulos Obtusángulos: entre los
tipos de triángulos, este se diferencia porque un ángulo es mayor a 90º

Área de un triángulo
El
área de un triángulo esta definida por la
formula:
base por altura divido por 2. La altura es la recta que va desde un vértice al lado opuesto, sin embargo en ocasiones que no conocemos alguno de estos dos datos podemos utilizar otras formulas.

Primero veremos un ejemplo sencillo:
Hallar el área del siguiente triángulo:

Área de un
triángulo equilátero Este ejemplo lo haremos con un triangulo equilátero del que solo conocemos sus lados. Tenemos la fórmula para hallar la altura:
Altura es igual a la
raíz cuadrada de 3 dividido por 2 por L (Un lado). También la fórmula para hallar el
área directamente: Área es igual a la
raíz cuadrada de 3 dividido por 4, por L (Lado) al cuadrado.

Ejemplo
Calcular el área de un triángulo equilátero de 10 cm de lado.

Área de un
triángulo rectángulo El área de un triángulo rectángulo es igual al producto de los catetos dividido por 2.

Ejemplo
Calcular el área del triángulo rectángulo cuyos catetos miden 3 y 4 cm.
 Semiperímetro
Semiperímetro El
semiperímetro de un triángulo es igual a la suma de sus lados partido por 2.
Se nombra con la letra
p.

Fórmula de
Herón La fórmula de
Herón se utiliza para hallar el área de un triángulo conociendo sus tres lados.

Ejemplo
Hallar el área del
triángulo cuyos lados miden 3, 4 y 5 cm.

Los triángulos se pueden clasificar según sus lados o según sus ángulos.
Tipos de triángulos según sus lados

- Triángulo equilátero: tiene todos sus lados iguales. Por tanto, sus ángulos también son los tres iguales. Es decir:

Como todos los ángulos son iguales y suman 180º (¿por qué suman 180º?), todos son de 60º (α=β=γ=60º).

- Triángulo isósceles: tiene dos lados iguales. Por lo tanto, dos de sus ángulos también son iguales.

El ángulo desigual β es el que forman los dos costados iguales (a y c).

- Triángulo escaleno: los tres lados son desiguales, por lo que los tres ángulos también son diferentes. Es decir:

Tipos de triángulos según sus ángulos
- Triángulo rectángulo: uno de sus ángulos es de 90º. Los otros dos son agudos (menores de 90º).
- Triángulo acutángulo: los tres ángulos son agudos (menores de 90º).
- Triángulo obtusángulo: uno de sus ángulos es mayor a 90º. Los otros dos son agudos (menores de 90º).

El perímetro de un triángulo rectángulo es la suma de los tres costados.


Ejemplo
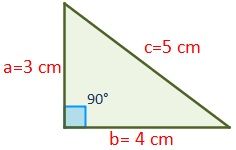
Sea un triángulo rectángulo con los tres lados conocidos, siendo éstos a=3 cm, b=4 cm y c=5 cm.
¿Cuál es su perímetro?
Éste se calculará como la suma de sus tres lados:

Y como resultado se obtiene que el perímetro es de 12 cm.
Perímetro de un triángulo rectángulo a partir del teorema de Pitágoras
El triángulo rectángulo cumple el teorema de Pitágoras, por lo que la hipotenusa (c) y el perímetro se pueden expresar a partir de los catetos (a y b).


Perímetro de un triángulo rectángulo a partir del teorema del cateto

El perímetro de un triángulo rectángulo se puede obtener a partir de la hipotenusa y las proyecciones de loscatetos sobre esta mediante el teorema del cateto.
Sean n y m las proyecciones de los catetos (b y a). Entonces el perímetro de un triángulo rectángulo viene definido por la siguiente fórmula:

Este método es útil si no se conocen los catetos (a y b).