Hola Compañer@s,  quiero compartir con ustedes este material sobre medidas de longitud.
La introducción al tema y algunos ejercicios para la practica.

Para medir longitudes se pueden utilizar distintas unidades de medida. La unidad de medida más utilizada es el metro (m). 

Se utiliza para medir la altura de un árbol, la longitud de una piscina,la longitud de una habitación, la altura de un edificio...

1.- Unidades menores 

Hay unidades de medidas menores que se utilizan para medir objetos pequeños (la longitud de un libro, de una goma, de un alfiler…). 

Decímetro (dm)

Centímetro (cm)

Milímetro (mm)

La relación con el metro es:

1 metro = 10 decímetros (si dividimos el metro en 10 partes iguales, cada parte es un decímetro)

1 metro = 100 centímetros (si dividimos el metro en 100 partes iguales, cada parte es un centímetro) 

1 metro = 1.000 milímetros (si dividimos el metro en 1.000 partes iguales, cada parte es un milímetro) 

La relación entre ellas es:

1 decímetro = 10 centímetros

1 decímetro = 100 milímetros 

1 centímetro = 10 milímetros 

 

2.- Unidades mayores

También hay unidades de medidas mayores que el metro que se utilizan para medir objetos o distancias grandes: la distancia entre 2 ciudades, la longitud de un río, la altura de las nubes….

Kilómetro (km)

Hectómetro (hm)

Decámetro (dam).

La relación con el metro es:

1 kilómetro = 1.000 metros

1 hectómetro = 100 metros 

1 decámetro = 10 metros 

La relación entre ellas también va de 10 en 10:

1 kilómetro = 10 hectómetros 

1 kilómetro = 100 decámetros 

1 hectómetro = 10 decámetros 

3.- ¿Cómo pasar de unidades mayores a unidades menores?

Para pasar de unidades mayores a unidades menores hay que multiplicar por 10 por cada nivel que descendamos:

Por ejemplo:

Para pasar de kilómetros a hectómetros hay que bajar 1 nivel por lo que tenemos que multiplicar: x 10.

Para pasar de kilómetros a metros hay que bajar 3 niveles por lo que tenemos que multiplicar: x 10 x 10 x 10, o lo que es lo mismo, hay que multiplicar x 1.000 

Para pasar de hectómetros a milímetros hay que bajar 5 niveles por lo que tenemos que multiplicar: x 10 x 10 x 10 x 10 x 10, o lo que es lo mismo, hay que multiplicar x 100.000 

 Veamos algunos ejemplos numéricos: 

¿Cuántos decímetros son 3 kilómetros? 3 x 10.000 = 30.000 decímetros 

¿Cuántos milímetros son 3 metros? 3 x 1.000 = 3.000 milímetros 

¿Cuántos centímetros son 3 metros? 3 x 100 = 300 centímetros 

¿Cuántos centímetros son 7 kilómetros? 7 x 100.000 = 700.000 centímetros 

¿Cuántos decámetros son 9 kilómetros? 9 x 100 = 900 decámetros 

¿Cuántos metros son 12 decámetros? 12 x 10 = 120 metros 

 

4.- ¿Cómo pasar de unidades menores a unidades mayores? 

Para pasar de unidades menores a unidades mayores hay que dividir por 10 por cada nivel que subamos:

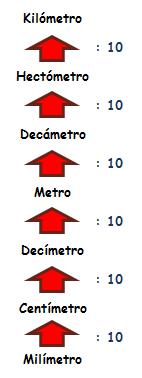
Por ejemplo:

Para pasar de metros a hectómetros hay que subir 2 niveles por lo que tenemos que dividir: 10 : 10, o lo que es lo mismo, hay que dividir entre 100

Para pasar de centímetros a kilómetros hay que subir 5 niveles por lo que tenemos que dividir: 10 : 10 : 10 : 10 : 10, o lo que es lo mismo hay que dividir entre 100.000 

Para pasar de decímetros a decámetros hay que subir 2 niveles por lo que tenemos que dividir 10 : 10, o lo que es lo mismo hay que dividir entre 100 

  Veamos algunos ejemplos numéricos: 

¿Cuántos metros son 7.000 milímetros? 7.000 : 1.000 = 7 metros

¿Cuántos kilómetros son 6.000 hectómetros? 6.000 : 10 = 600 kilómetros 

¿Cuántos metros son 8.000 centímetros? 8.000 : 100 = 80 metros 

¿Cuántos hectómetros son 200 decímetros? 200 : 1.000 = 0,2 hectómetros 

¿Cuántos decímetros son 5.000 milímetros? 5.000 : 100 = 50 decímetros 

¿Cuántos decámetros son 120 decímetros? 120 : 100 = 1,2 decámetros

Ejercicio s

1. Calcula las siguientes conversiones:

1) 7 m = ____ mm  

2) 8 dm = ____  cm  

3) 13 cm = ____  mm  

4) 21 m = ____  mm  

5) 13 m = ____  mm  

6) 21 m = ____  dm  

7) 7 dm = ____  cm  

8) 8 cm = ____  mm  

9) 7 m = ____  dm  

10) 15 dm = ____  mm  

11) 6 km = ____  m  

12) 9 hm = ____  dam  

13) 13 dam = ____  m  

14) 15 km = ____  dam  

15) 18 dam = ____  m  

16) 25 hm = ____  dam  

17) 12 km = ____  hm  

18) 11 dam = ____  m  

19) 14 km = ____  hm  

20) 10 hm = ____  m  

21) 8 km = ____  dm  

22) 9 dm = ____  mm  

23) 11 dam = ____  dm  

24) 18 hm = ____  dm  

25) 19 m = ____   mm  

26) 31 hm =   ____  mm  

27) 7 dam = ____  cm  

28) 9 cm = ____  mm  

29) 17 dam = ____  cm  

30) 7 km = ____  dam

Expresa en las unidades indicadas:

1)  25 m = ________ cm =   ________ dam =   ________ mm. 

2)  78.9 hm = ________ m =   ________ cm =   ________ Km. 

3)  0.592 Km = ________ m =   ________ dam =   ________ dm. 

4)  37.45 dm = ________ hm =   ________ dam =   ________ cm. 

5)  0.102 m = ________ dm =   ________ dam =   ________ cm. 

6)  23.911 Km = ________ dm =   ________ hm =   ________ m.

Resuelve los problema

Julia y Aitana están pensando hacer un viaje en ruta este verano, pero aún no saben cuál. Tienen que tener cuidado porque, aunque en el mapa las distancias parecen muy cortas, 9 cm del mapa equivalen a 90.000 m. Han visto una ruta muy interesante que, en el mapa, se extiende 20 cm. ¿Cuál es la longitud real de la ruta que han visto?  

Expresa el resultado en km
La longitud real de la ruta es de ________ km 

Expresa el resultado en hm
La longitud real de la ruta es de _________ hm

Problema del Pirata 

Un Pirata ha llegado a la isla del Coral para buscar un tesoro. En el mapa pone que, desde la orilla, debe recorrer 3,7 hm  hacia el centro de la isla, donde hay una palmera y después otros 8,5 dam en la misma dirección. 

¿Cuántos metros recorrerá en total desde la orilla hasta el tesoro? Expresa el resultado también en kilómetros.

Problema de la melena

¡Qué pelo más bonito tiene Gabriela! Antes era la chica que más largo tenía el pelo de toda la clase: la melena le medía 6 decímetros de longitud. Pero ayer se lo cortó 25 centímetros, así que ahora la chica con el pelo más largo de la clase es María.
¿Cuántos centímetros mide la melena de Gabriela ahora?
Expresa el resultado también en milímetros.


Problema del oso y la miel

Un oso al que le encanta la miel quiere sacar miel de una colmena que hay en la rama de un árbol, pero está demasiado alta. Para alcanzarla, se sube en una roca de 12 dm de alto que hay justo debajo y, con las garras muy estiradas, llega justo a cogerla. Si este oso cuando se estira mide exactamente 2,3 m,
¿a qué distancia del suelo estaba exactamente la colmena?
Expresa el resultado en metros y en centimetros.

Relaciona.
0,8 m                                     80 dm
8 m                                        0.008 hm  
80 m                                      80 hm
8.000 m                                8.000 cm