Hola Compañer@s, les traigo unos problemas matemáticos para ponernos a prueba a nosotros y a nuestros alumnos.
Es una gran actividad que siempre atrapa a mis estudiantes... tanto, que algunos tratan de resolverlos incluso durante los recreos.

Este problema matemático de hace 20 años sólo lo supo resolver el 10% de los estudiantes de 16 países de todo el mundo (el 4% en Estados Unidos y el 24% en Suecia). Se trata de uno de los tres problemas que la Asociación Internacional para la Evaluación de Logros Académicos (IEA), propuso a estudiantes de secundaria de matemáticas avanzadas. La asociación explicó que este problema fue el que más gente falló, a pesar de que no hace falta saber muchas matemáticas, al igual que ocurría con el problema de lógica del cumpleaños de Cheryl.

Su enunciado es en apariencia sencillo: “Una cuerda está enrollada de forma simétrica alrededor de una barra circular. La cuerda da la vuelta exactamente cuatro veces alrededor de la barra, que tiene una circunferencia de 4 centímetros y una longitud de 12 centímetros. Averigua cuánto mide la cuerda".

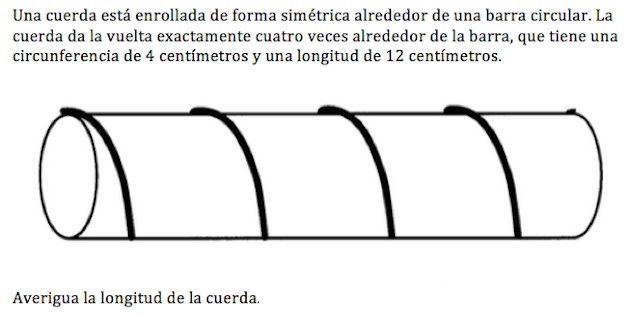
Solución

El problema no requiere saber más matemáticas que el teorema de Pitágoras: en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Como se puede ver en la ilustración de la IEA, la forma más fácil de resolverlo es pensar en la barra como en una superficie plana. De este modo, vemos que en los extremos se forma un triángulo rectángulo. Sabemos que uno de los catetos mide cuatro centímetros y el otro, tres (una cuarta parte de la longitud de la barra), lo cual nos permite averiguar cuánto mide la hipotenusa. Este resultado nos basta para saber la longitud de la cuerda, ya que hay cuatro trozos iguales alrededor de la barra.

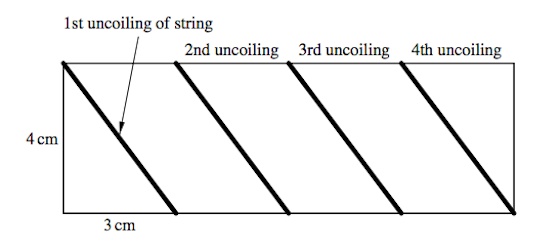
La hipotenusa es igual a la raíz cuadrada de 42 + 32. Es decir, a la raíz cuadrada de 25 (16+9), que es cinco. Como hay cuatro trozos iguales a lo largo del cilindro, la cuerda mide 20 centímetros (5*4).

Desde la IEA se explicaba que los alumnos tuvieron problemas para encontrar la equivalencia entre esta cuerda enrollada y un triángulo porque “aprender a pensar de esta forma creativa y aplicada no forma parte de ningún currículum”.

El cumpleaños de Cheryl

Solución

1. Esto es lo que sabemos: Cheryl ofrece una lista de fechas. A Albert solo le ha desvelado 
el mes de su cumpleaños y a Bernard el día.

Pensemos como Albert: si el día del cumpleaños fuera el 18 o el 19, Bernard sabría la solución a la primera porque con ese número solo existen dos opciones, el 19 de mayo y el 18 de junio. Esta lógica le permite hacer un segundo descarte: todas las fechas de mayo y junio, porque él conoce el mes y la única opción de estar seguro de que Bernard no lo sabe es porque el mes es otro.

2. Siguiendo la lógica de Albert y eliminadas todas las opciones de mayo y junio, Bernard ahora sí sabe cuándo es el cumpleaños de Cheryl. ¿Qué podemos deducir de esto? Que no puede ser el 14 porque se repite en julio y agosto y para estar totalmente seguro tiene que ser uno de los días únicos: el 16 de julio, el 15 y el 17 de agosto.

3. Si Bernard lo sabe, ahora Albert también. Y ade ahí nosotros deducimos que si el mes fuera agosto, Albert no lo sabría porque tiene dos opciones, así que la única y obvia solución es el 16 de julio.

Un profesor explicó  que sus niños lo acertaban a la primera pero que los adultos a los que se lo enseñaba podían pasar horas dándole vueltas sin resolverlo.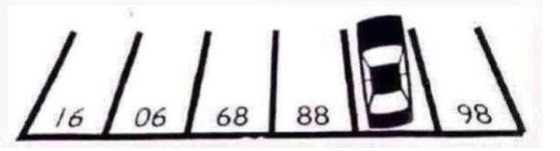

En la foto aparecen seis plazas de parking numeradas. 

La pregunta es: Â¿en qué número está aparcado el coche?

 .

.

.

.

 

Solución

La respuesta en realidad es muy sencilla. Solo hay que coger la imagen y darle la vuelta. Al girar los números vemos que son consecutivos: 86, 87, 88, 89 y la respuesta es evidente.

Espero les hayan gustado y los compartan con sus alumnos y colegas a ver quien puede resolverlos! :)

Unete a la comunidad y comparte material, recursos e ideas!