Buenas colegas, hoy vamos a conocer 3 métodos fantásticos para aprender a multiplicar cifras grandes sin utilizar calculadora. De esta manera permitirán que sus estudiantes encuentren la manera más sencilla y divertida de resolver estas operaciones.

1. El método japonés 

Conocí este método cuando me lo enseñó uno de mis alumnos y desde entonces no he dejado de utilizarlo, pues su simpleza y claridad pictórica asegura que ningún estudiante se quede detrás

Dejo aquí el video que creo y una breve explicación que les permitirá comprenderlo rápidamente

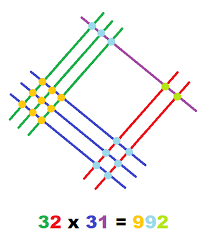
El método consiste en dibujar rectas paralelas y perpendiculares para representar los dígitos de los números a multiplicar.

Tomemos por ejemplo 23 x 41.

Dibujamos dos líneas paralelas para representar el 2 y otras tres líneas paralelas para el 3.

Luego perpendicularmente dibujamos cuatro líneas paralelas para el 4 y una línea para el 1.

A continuación, una vez que tenemos nuestra imagen, se suman los puntos que se forman en las intersecciones.

Y así obtenemos como resultado 943, el mismo que la forma tradicional de multiplicar.

Sencillo ¿verdad?

2. El método hindú 

Este método lo he descubierto más recientemente pero ha comprobado ser de mucha utilidad para motivar a algun@s de mis estudiantes que no terminaban de comprender los métodos clásicos. He dedicado un post especial a este método donde podrán encontrar actividades y hojas de trabajo listas para imprimir ¡siempre es mejor jugando! --> Método Hindú + Actividades <-- 

 

En este método de multiplicación tenemos que construir una tabla.

Vamos a usar el mismo ejemplo de antes: 23 x 41. 

Entonces, dibujamos una tabla con cuatro casilleros: uno por cada dígito que tenemos en nuestro cálculo. 

Y partimos cada cuadro con una línea oblicua. 

Entonces empezamos multiplicando los primeros dígitos de ambos números: el 2 con el 4, colocando un 0 en el primer triángulo y un 8 en el segundo. 

Luego multiplicamos el 2 con el 1 y colocamos el 0 en el primer triángulo y el 2 en el segundo. 

Y hacemos lo mismo con los dos dígitos del segundo número de nuestro cálculo. 

Una vez que tenemos todos los casilleros completos, hacemos una suma en diagonal.

¡Eso es todo!

3. Método Array 

Este método también tiene una propuesta propuesta con cuadrilla, sin embargo, es bastante diferente del método hindú. Este breve video explicativo lo aclara a la perfección. De los anteriores es el más difícil pero entiendo que hay personas con todo tipo de gustos y facilidades ;)

Seguimos con el ejemplo 23 x 41. 

Aquí descomponemos el número. Es decir en un cuadro colocamos 20 y en el otro 3. 

Mientras que en los cuadros verticales colocamos 40 en el primero y 1 en el segundo. 

Entonces multiplicamos los números de cada casillero con el contrario. 

Sin embargo, ignoramos si hay 0. 

Por lo tanto, en vez de multiplicar 20 x 40, suprimimos los 0 y solo calculamos 2 x 4 obteniendo 8.

Lo mismo con 3 x 40. Eliminamos el 0 y multiplicamos 3 x 4 que nos da como resultado 12. 

Hacemos lo mismo con los casilleros de abajo. 

Y ahora sumamos los 0 que habíamos dejado de lado. 

Entonces al primer cálculo que era 20 x 40 y obtuvimos 8, le sumamos dos ceros y nos da 800. 

Al 3 x 40 que nos dio 12, le agregamos un 0 y nos queda 120. 

Y así sucesivamente con el resto de los casilleros en los cuales suprimimos anteriormente los 0. 

Y finalmente sumamos los cuatro números que nos quedaron como resultado en cada uno de los casilleros. 

¿Has comprendido con los ejemplos? Espero que sí

¡A practicar se ha dicho!