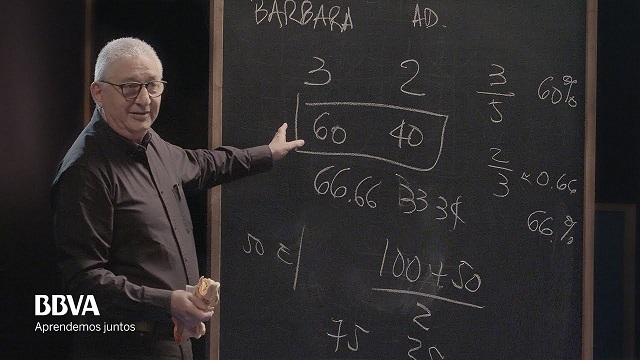
Hola Colegas, como están?
Les dejo esta genial charla de Adrián Paenza para compartir con colegas y alumnos. Vale la pena cada segundo... Al final también les dejo algunos problemas para pensar y compartir :)

¿Las matemáticas pueden ser divertidas? ¿Cómo pueden ayudarnos en nuestro día a día? En definitiva, ¿cuál es el poder que nos da las matemáticas? Nadie mejor que Adrián Paenza para responder a estas preguntas. Doctor en matemáticas y profesor en la Universidad de Buenos Aires durante más de 20 años, Paenza está considerado como uno de los grandes divulgadores matemáticos del mundo, recibiendo, entre otros, el prestigioso premio Leelavati en 2014 otorgado por la Unión Matemática Internacional, por su contribución y labor divulgativa.

Su pasión por ciencia, la política y el deporte le llevó, a compaginar su faceta como matemático con el periodismo. Profesión que ha desarrollado con éxito durante más de cuarenta años en los grandes medios argentinos de prensa, radio y televisión en la que destacaron los populares programas: Científicos Industria Argentina y especialmente Alterados por Pi, programa que se mantuvo en antena durante más de diez años.

Es autor de numerosos libros, entre los que destacan la exitosa serie: Matemática, ¿estás ahí?, Matemagia (2015), Matemáticas para todos (2017) y La puerta equivocada (2018). A través de historias, retos y enigmas, Adrián Paenza logra despertar nuestra curiosidad, desafiar nuestra imaginación y contagiarnos su entusiasmo por el conocimiento y el aprendizaje, demostrando que las matemáticas además de muy útiles son tremendamente divertidas.

Les dejo un fragmento para que vean de que se trata

¿Cuál es el gran poder de las matemáticas?

Versión Completa. Matemáticas para la vida real.

1. Dos pintores y una pieza 

2. ¿Da lo mismo subir que bajar un 40%?

3. Problema de los seis fósforos

1. Dos pintores y una pieza

En una casa hay una habitación grande que hay que pintar. Un pintor, llamémoslo A, tarda 4 horas en pintarla solo. El otro, a quien llamaremos B, tarda 2 horas.

¿Cuánto tardarían si los dos se pusieran a pintarla juntos?

(Antes de avanzar: la respuesta no es 3 horas.)

Solución

La tentación es decir que si trabajan los dos juntos van a tardar 3 horas en pintar la pieza. Sin embargo, uno contesta eso porque, en principio, no está pensando. Basta advertir que, si uno de los dos pintores trabajando solo tardaría 2 horas, no es posible que con ayuda de otro ¡tarden más!

Estoy seguro de que hay muchísimas maneras de llegar a la solución. Más aún: ni siquiera creo que las dos que voy a proponer sean las mejores. Es decir: lo invito a que imagine una respuesta que sea atractiva por lo breve y contundente. Por eso es que creo que no vale la pena leer lo que figura más abajo... Pero, si aun así usted insiste, aquí va.

Le propongo pensar lo siguiente. En una hora, el pintor que pinta más rápido, B, pinta la mitad de la pieza. El otro, A, mientras tanto, pinta una cuarta parte (ya que, como tarda 4 horas en pintar todo, en una hora pinta justo la cuarta parte de la pieza).

Ahora bien, hasta acá, entre los dos pintaron las tres cuartas partes. Relea lo que acabo de escribir: tres cuartas partes. O sea, tres veces una cuarta parte (eso es lo que significa tres cuartos de algo). Y tardaron una hora en hacerlo. Por lo tanto, como queda una cuarta parte por pintar, les hace falta la tercera parte de una hora. Piénselo conmigo otra vez: si en una hora pintaron tres cuartos, para pintar un cuarto (que es la tercera parte de 3/4), les hace falta usar la tercera parte de una hora, o sea, 20 minutos.

Los dos pintores juntos tardarán 1 hora y 20 minutos para pintar la pieza.

También podemos pensar el problema usando lo que nos enseñaron en el colegio como "regla de tres simple". Como hice en la solución 1, sabemos que en una hora pintan 3/4 partes de la pieza. La pregunta es, entonces, ¿cuánto tardarán en pintar toda la pieza? Y para eso escribimos:

3/4 pieza → 60 minutos

1 pieza → x minutos

Para "despejar" la x (o para "calcular" la x), hacemos

x = (1 * 60)/(3/4) = 60/(3/4) = (4/3) * 60 = 80

Luego, en total, entre los dos tardarán 80 minutos, o sea, 1 hora y 20 minutos.

2. ¿Da lo mismo subir que bajar un 40%?

Algunas preguntas sobre porcentajes.

Si uno empieza con un número cualquiera, digamos 100, y le quita el 40%, y al resultado lo incrementa un 40%, ¿se llega otra vez a 100?

Al revés ahora: si uno empieza con el número 100, le agrega un 40%, y al resultado le descuenta ahora un 40%, ¿se llega otra vez a 100?

Las respuestas que dio para las dos preguntas anteriores, ¿dependieron de que empezara con el número 100, o habría dado lo mismo si hubiera empezado con cualquier otro número?

Y las respuestas que dio para las dos primeras preguntas, ¿dependieron de que fuera un 40%, o habría dado lo mismo con cualquier otro porcentaje?

Si uno incrementa un número en el 100% y luego descuenta el 100%, ¿se tiene el mismo número con el que empezó? Y al revés, si uno descuenta el 100% y luego lo aumenta, ¿qué obtiene?

Supongamos que tiene que pesar exactamente diez kilos de azúcar. Para lograrlo, se tienen dos pesas de cinco kilos cada una, y una balanza con dos platillos.

La dificultad reside en que la balanza está desbalanceada. Esto significa que, sin que haya ningún peso en ninguno de los dos platillos, hay uno que está más arriba que el otro.

¿Cómo hacer?

Solución

Si usted hizo las cuentas, habrá advertido que ¡no da lo mismo! Es decir, si al número 100 uno le descuenta un 40%, se obtiene el número 60. Si ahora, uno incrementa un 40% al número 60, se obtiene el número 84. Es decir, no da lo mismo deducir un 40% del número 100 y luego aumentárselo.

De la misma forma, si uno empieza primero agregando un 40% al número 100, obtiene el número 140. Si luego a este número (140) le descuenta un 40% (haga la cuenta acá antes de seguir leyendo), el resultado es 84. Es decir, tampoco se vuelve al número 100 de partida.

Por un instante, quiero hacer una cuenta que abarque MÁS que al número 100. Si uno empieza con un número A cualquiera, si primero le aumenta un 40% y luego, al número que obtuvo, le deduce un 40%, no vuelve al mismo número. Y lo mismo sucede al revés, si uno empieza deduciendo primero y aumentando después.

¿Cómo se puede demostrar esto en general?

Para descontar el 40% de un número A lo que hay que hacer es:

(0,6) * A → (1)

en realidad, calcula el 60% de A, pero es exactamente lo que uno quiere, porque queremos saber a qué número se llega primero cuando uno descuenta el 40% del número A.

Para incrementar un 40% a un número B cualquiera, lo que hay que hacer es:

(1,4) * B → (2)

Luego, usando los resultados de (1) y (2), se tiene:

Situación inicial A

Descuento el 40% (0,6) * A

Aumento el 40% a este número (1,4) * (0,6) * A

Y este último número es

(1,4) * (0,6) * A = (0,84) * A → (3)

Luego, no se vuelve al número A original, sino a (0,84) * A, que es 16% menor que el que había al principio.

Si uno va para el otro lado, es decir, comienza incrementando un 40%, se tiene:

Situación inicial A

Incremento el 40% (1,4) * A

Descuento el 40% a este número (0,6) * (1,4) * A

Este último número es el mismo que teníamos en (3), pero uno descubre que no se obtiene A sino un 84% de A. O sea,

(0,6) * (1,4) * A = (0,84) * A → (4)

Luego, la respuesta a las dos primeras preguntas es que no se vuelve al número original. Lo que sí sucede (interesante) es que, si uno ganara en el casino un 40% del dinero que llevó y luego pierde un 40%, si bien no llegará al mismo número con el que empezó (porque perdió un 16%), llegará al mismo número que si hubiera empezado perdiendo un 40% y luego recuperando el 40%.

Para contestar a la tercera pregunta, es fácil comprender que, si en lugar de haber usado el 40% hubiera tomado cualquier otro porcentaje, el resultado sería el mismo. El número 40 es un número cualquiera que elegí para hacer la pregunta, pero habría servido cualquier otro.

Lo invito a pensar en algo más: si al final del proceso uno termina descontando el 100%, el resultado final tiene que ser ¡cero! Luego, si uno empieza con cualquier número A y lo incrementa en un 100% (o sea, lo multiplica por dos), y luego, al resultado (que es 2A) le descuenta el 100%, lo que se obtiene es... ¡cero! Y lo mismo pasa para el otro lado. Incluso más rápido. Porque si uno empieza con A y le descuenta el 100%, se queda con cero. Aunque ahora uno pretenda aumentar el 100%, lo que tendrá seguirá siendo cero. Sin embargo, el número A no se recupera más. ¿No resulta interesante todo esto?

3. Problema de los seis fósforos

Se tienen seis fósforos iguales. ¿Es posible construir con ellos cuatro triángulos equiláteros cuyos lados sean iguales al largo del fósforo?

Nota 1: No conteste rápido si no se le ocurre la solución. Piense.

Nota 2: Triángulo equilátero quiere decir que tiene los tres lados iguales. De hecho, "equi" = "igual", "látero" = lado. En este caso, lados iguales y, además, de igual longitud que la del fósforo.

Solución

No sé si a usted se le ocurrió (o no) la solución de este problema. En cualquier caso, nos pone a prueba.

Si contestó que no, que no se pueden construir los cuatro triángulos, su respuesta es incorrecta. Pero tiene una explicación, algo que nos sucede a la mayoría de los humanos. Uno busca, dibuja, hace gráficos y se desespera porque no puede encontrar la respuesta.

Es que el problema no tiene solución... ¡en el plano! Es decir, si usted intentó hacer un dibujo en un papel, o si tomó los fósforos de verdad y quiso encontrar la manera de formar los triángulos, haciendo distintos intentos en una mesa o escritorio, no pudo. Lo que pasa es que, para dar con la solución, lo que hay que hacer es salirse del plano y pensar en tres dimensiones. En realidad, lo que hay que hacer es pensar (y construir... Hágalo usted solo/a) una pirámide con base triangular.

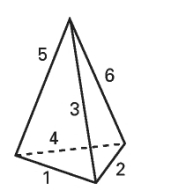
En este caso, si cuenta cada cara de la pirámide, resulta ser un triángulo, y como hay cuatro caras, entonces, hay cuatro triángulos equiláteros, que es exactamente lo que queríamos.

¿Qué enseña esto? Que si uno no sale de la dimensión en la que se encuentra, es imposible que encuentre la solución. Nos enseña a pensar distinto, a no quedar restringido o atrapado sólo en lo que uno ve. Peor aún: uno tiene la tentación de abdicar, y de decir que el problema no tiene solución, cuando en realidad sí tiene... sólo que no la encontrará donde usted la estaba buscando. Ni yo.

----------------------------------------------------